 What were you thinking?
What were you thinking?The best student in my elementary algebra class looked up from the last page of the exam and tried to kill me with her eyes. It startled me. Surely, of all people, she should have taken it in stride. She picked up her exam and came forward to see me. “We never did these,” she said.
I understood. That exact problem had not appeared in either the homework or any of the quizzes. She seriously judged the exercise to be out of bounds. I had betrayed their trust.
How egregious was my crime? Consider: The exam was on systems of linear equations. All of the problems were limited to two equations with two unknowns. (This is elementary algebra, after all.) We had solved systems by graphing the lines and checking the results by substitution (just a glorified version of “guess & check”—and limited to cases with really simple solutions). We had solved systems by solving one equation for a variable and substituting the result into the second equation. Finally, we had solved systems by adding the equations (or their equivalents) so that one of the variables was eliminated.
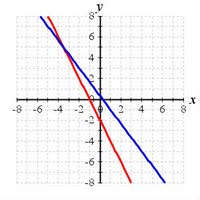 My students were dismayed that the last problem on the exam was not precisely any of these. Instead I had presented them with a graph that displayed two lines:
My students were dismayed that the last problem on the exam was not precisely any of these. Instead I had presented them with a graph that displayed two lines: Find the equations of the two lines in the figure and then solve the corresponding system of equations to determine where they cross.This problem turned into one of the starkest discriminators ever between my strongest and weakest students. The best student in class, who had forthrightly expressed her dismay, calmed down as soon as I asked her if she knew how to find the equation of a line. “Yes, sure, if I know some points on the line.” “Well,” I said, “I've given you lots to pick from if you can read a graph.”
 We had read many graphs in the previous chapters on linear functions and equations. We had worked lots of problems involving finding slopes and equations of lines. I was expecting them to remember how all of that work was related to the content of the current chapter, especially since we had never stopped doing such exercises. A few students just gave up. A few more tried to read the intersection point from the graph but abandoned any attempt to find the actual equations of the system. (They got a few points if they correctly read the intersection coordinates.) A handful realized that they knew everything they needed to solve the problem in detail. Both lines intersected several grid nodes. (I wonder what would have occurred if I had highlighted those points as in the accompanying figure.)
We had read many graphs in the previous chapters on linear functions and equations. We had worked lots of problems involving finding slopes and equations of lines. I was expecting them to remember how all of that work was related to the content of the current chapter, especially since we had never stopped doing such exercises. A few students just gave up. A few more tried to read the intersection point from the graph but abandoned any attempt to find the actual equations of the system. (They got a few points if they correctly read the intersection coordinates.) A handful realized that they knew everything they needed to solve the problem in detail. Both lines intersected several grid nodes. (I wonder what would have occurred if I had highlighted those points as in the accompanying figure.) After I had graded the exam, I noticed that the infamous exercise had turned into something very close to an all-or-nothing situation for most of my students. Either they received a meager number of points for their futile (or nonexistent) efforts or they raked in virtually all of the points possible on the problem. Only six managed an A on the problem, while three were at the D level and twenty-five bombed it outright. The table shows how the students who earned 90% or more of the credit on the crossed-lines problem tended to be A students. When I checked my records for the one exception—the C student—I discovered that he was a chronic class-cutter. He seemed to know his stuff but had missed almost all the quizzes and taken a big hit on his course grade because of his lower overall point total. In other words, high performance on this one problem was a sure indicator in this class of high-level algebra skills. However, it simply split the class into two camps with no gradations in between: the A students versus everyone else. As I said before in a slightly different context, it was essentially all or nothing. (Of course, we should note that the problem grade and the course grade are hardly independent of each other since the latter incorporates the points earned on the former. Still, by this point in the semester a single problem on one exam has only a small effect on the cumulative grade.)
After I had graded the exam, I noticed that the infamous exercise had turned into something very close to an all-or-nothing situation for most of my students. Either they received a meager number of points for their futile (or nonexistent) efforts or they raked in virtually all of the points possible on the problem. Only six managed an A on the problem, while three were at the D level and twenty-five bombed it outright. The table shows how the students who earned 90% or more of the credit on the crossed-lines problem tended to be A students. When I checked my records for the one exception—the C student—I discovered that he was a chronic class-cutter. He seemed to know his stuff but had missed almost all the quizzes and taken a big hit on his course grade because of his lower overall point total. In other words, high performance on this one problem was a sure indicator in this class of high-level algebra skills. However, it simply split the class into two camps with no gradations in between: the A students versus everyone else. As I said before in a slightly different context, it was essentially all or nothing. (Of course, we should note that the problem grade and the course grade are hardly independent of each other since the latter incorporates the points earned on the former. Still, by this point in the semester a single problem on one exam has only a small effect on the cumulative grade.)My students and I reviewed all the problems and their solutions when I returned the exam. Some of them commented on how similar the problem was—in retrospect—to earlier quiz and exam problems where they had been required to compute slopes by reading points from the coordinate grid. I won't claim that they were happy about it, but they had at least recognized that the problem was not as shockingly new as they had originally thought. Now they're expecting a follow-up quiz that will give them an opportunity to earn points by demonstrating they learned the lesson of the algebra problem from hell. I won't disappoint them and I hope that they won't disappoint me.










8 comments:
A question from a current math major and probable future math teacher: you
focus on how this question effectively discriminated between those who
"get it" and those who don't -- in your opinion, does that make this a
"good problem?" (Or, in fact, do you have any value judgements about
either it or related things?)
JBL
(Sorry about the spacing there.)
Yes, this was a "good" problem, but in a very specific, narrow sense. I wish I could write such problems at will because they seem to be good tools for finding out which of my students really "get" it when it comes to the course material. Let's not oversell it, though, because the effect of this problem was to confirm that my A students were indeed set apart from their classmates; apparently the chapter tests were already succeeding at identifying them.
It would be a very bad idea to try to make all quiz and test problems function like this kind of "high-pass filter". It would demoralize the students and would defeat the primary purpose of getting as many students as possible through the course with as much comprehension as possible. I'm suppose to help students raise their level of understanding, not pick out the handful who already know what's going on.
Thanks for the comment and good luck in your pursuit of a teaching career.
I teach formal logic and found the same basic situation in my classes. Students are able to do problems similar to their homework problems, but not problems that required integration of all their logical tools. I also found that students were getting As in the course while not being able to do the more complex problems.
I also found out that not all students WANT an A, many are happy with a B -- but they are afraid to leave some problems on a traditional exam undone, and it simply stresses them out.
With these factors in mind, I revised my final exam to have three tiers, one of C problems, one of B problems and one of A problems. In order to get an A, they need to complete the A problems, for a B the B problems etc.
itpf: How do you implement that? Do the students know which problems are which? And when you say, "to get an A, they need to complete the A problems," does that also mean they need to complete the B and C problems?
(An anecdote: a couple of summers ago I worked at a math camp for talented high school students. In the most advanced class, we would give them several very challenging problems each week and everyone would write up their solutions. There were two separate grading schemes employed, one of which assigned a fixed number of points to the entire class for each problem. Thus, if only one person solved the question she would collect all of the points, while if everyone solved it they would split it evenly.)
I've been a big participant in (and occasional creator of) math competitions for high school students, and as a result I've developed a real appreciation for the sort of problem that has that effect. On the other hand, I don't think I would enjoy being a student in a class where all the questions were like that, even if one were at the top of the class.
I don't really have a point here so much as a lot of loosely connected thoughts, so I think I'll end my rambling with that.
Students, I am told, need wake-up-calls and welcome-to-college experiences. I give take home quizzes that basically set my expecations. But boy does this require tenacity. I have to give low scores on several projects before there is a sense of the expecation, thinking is required.
Too true. Quite a few of them have yet to attain the college student frame of mind. Instead I get whiny complaints about "too many quizzes" and (one of my personal favorites) pleas for "extra credit". Of course they need the "extra" credit because they neglected to collect much of the credit that's regularly available in class or via homework, so they figure I should gin up some special projects to permit them to compensate for missing class or otherwise blowing off assignments. {sigh} Sorry. No extra credit. Come to class. Do your assignments. Be a student.
I agree students need to be more concerned with the credit portion of the class and less concerned with the extra credit. That's why when asked for extra credit I simply give them extra non-credit.
Post a Comment