Lucky Larry hits a grand slam
It has been noted that state lotteries are basically a tax on innumeracy. You're better off dealing with the house percentage at a casino in Nevada. Nevertheless, even lotteries have winners. Just don't expect it to be you. Lightning is not going to strike you.
Of course, sometimes it strikes near by.
One of my students won the calculus lottery during the exam on integration, beating very long odds indeed. The result was the most bizarre “Lucky Larry” of my years as a math teacher. My colleagues were as flabbergasted as I was when I shared the student's “solutions” with them. Her work was nonsense, yet her answers were correct. Three times in a row. Of course, when that happens one suspects a hidden underlying pattern that produces valid results, contrary to all expectations. In this case, though—no. It was a giant fluke.
Or, rather, three flukes in a row. My flabber, she is as gasted as possible.
The problem on the integration exam was one of my “conceptual” exercises. One of my tasks as a calculus teacher is to clarify the meaning of the definite integral, ensuring that my students grasp its significance. Of course, one of the most common (and visual) interpretations of the definite integral is as the area under a curve. Surely any first-year calculus student must understand at least that much.
Accordingly, I presented my students with the graph of a simple function and asked them to evaluate three definite integrals of that function by inspection of the graph. I did not forbid them to use antidifferentiation and the fundamental theorem of calculus, but I emphasized that the simplest of calculations would suffice.
What, pray tell, is the value of the definite integral of f(x) from x = 1 to x = 2? A cursory examination of the trapezoidal region spanning the space between the x axis and the graph of the function reveals the area (and thus the definite integral) to equal 1.5. Easy! Not satisfied, however, with such a trivial computation, one of my students rolled out the big guns:
Damn! What a coincidence! The calculus is bogus, but the result is accidentally correct. No one expects lightning to strike twice, of course.
Brace yourself.
What if we ask for the definite integral from 1 to 3 instead? We get a little more area now. Take a look at the new graph, in which a second trapezoid now joins the first. We get an additional 2.5 square units which, added to the original 1.5, gives us 4. My student swung into action and unlimbered her surreal calculus calculation again:
I was now quite beside myself, shaking my head in astonishment as my red pen hovered over the page. Twice in a row! (What were the odds?)
Fortunately, I knew that I could count on part (c) to set the record straight and demonstrate to my student the error of her ways. It was, in fact, the simplest part of the problem. A kind of gift to the student possessing a clue. Can you find the area of a rectangle measuring 2 by 4? Of course! The answer must be 8.
My student presented her solution:
Nooooooooo!
Time to hit my head against the desk a few times.
In a million years, this will never happen again. (For one thing, this problem is going straight into the waste can, never to be recycled.)
I need to go lie down for a few minutes.
Wednesday, December 14, 2011
Subscribe to:
Post Comments (Atom)


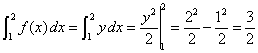
















14 comments:
That's hilarious!
Your graph and chosen integration regions match up perfectly to your student's consistent misunderstanding. Also, it's possible that the student noticed that their answers matched the number of squares, which is what you were looking for, but they didn't bother writing down the observation since they "answered" the problem with the more mathsy calculus.
So how did you mark it?
Full disclosure, Simon: Two of my students fell down this particular rabbit hole on this particular problem. The guy's "solutions" consisted solely of the bogus definite integrals. He got very little credit. (Perhaps he also eyeballed the graphs and saw that his answers were consistent with them, but he did not say so.) The gal accompanied her bogus integrals with notes that pointed out the simple geometric computations as an alternative. She earned most of the points, with a few deducted for the calculus bogosity.
hahahahaha *takes breath* hahahaha!
...
*Stops, realizes her students are taking a final, and she shouldn't tempt fate right now*
It's hard for a smart person to anticipate the vast potential for stupidity.
I wish my calculus professor would ask me questions as easy as these.
Or maybe not, I would drive myself crazy looking for the catch...
Some of the other problems were just a bit more challenging, Sophia.
This teaches us one thing: when in doubt, integrate y dx! Hehee
...Do you suppose she was messing with you?
Perhaps while doing homework earlier in the term, she used this bogomath by mistake and noticed that it worked under certain circumstances. So she decided to have a little fun with you on the exam.
Prudence would dictate doing it on homework instead, with less of the grade at stake, but maybe she was doing well enough that she could afford to risk some points on this exam.
Are the rest of her grades consistent with this interpretation?
No, Tualha, she wasn't messing with me. I'm quite certain she had no idea her calculations were invalid. Joshing around with coincidentally correct bogus math would have been completely uncharacteristic of her.
The geometric reason why this allegedly "stupid" calculation actually works is of course the fact that your blue curve is - at least in the relevant range between x=1 and x=5 - perfectly symmetrically aligned with respect to the curve y=x, so the two curves give the same integral value.
Greetings from Bonn (in Germany),
Daniel
Du hast recht, Daniel. Amusing, isn't it? If only I hadn't used the function I used, or the intervals I chose. Weird, weird coincidence.
If it makes you feel any better, I solved a university calculus problem by taking the average of two infinities. It was a bogus problem, anyway.
This is awesome!
Simply shocking. It seems, that your students' basic problem is to determine the linear function, whyich are, subsequently f(x)=-x=3, f(x)=3x-5 and f(x)=3. This should be have done a way long before the elementary integrating was introduced (as I remember, in Poland children are taught this in the age of 12), Let alone the Pytagorean theorem if you really did not bother about the method.. Greetings from Bridgwater.
Post a Comment